几何平均收益率
网友投稿• 2021-12-20 04:41:56 •阅读45
什么是几何平均收益率 几何平均收益率是将各个单个期间的收益率乘积,然后开n次方。几何平均收益率使用了复利的思想,即考虑了资金的时间价值,也就是说,期初投资1元,第一期末则值(1 + R1)元,第二期投资者会将(1 + R1)进行再投资,到第二期末价值则为(1 + R1)(1 + R2)元,……。 这个平均收益指标优于算术平均收益率,因为它引入了复利的程式,即通过对时间进行加权来衡量最初投资价值的复合增值率,从而克服了算术平均收益率有时会出现的上偏倾向。 几何平均收益率的公式 如果Rij表示资产组合j的第i个可能的收益率,且每一结果的可能性相同,那么该资产组合的几何平均收益率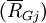 为:
为: 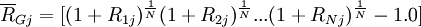 如果每个观察值的可能性不同,Pij是第i个收益率的概率,那么几何平均收益率为:
如果每个观察值的可能性不同,Pij是第i个收益率的概率,那么几何平均收益率为: 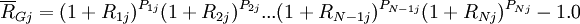 用符号
用符号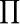 表示乘积,上式可写为:
表示乘积,上式可写为: 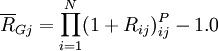 几何平均收益率的例子 例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%,第2年的投资收益率则为-50%。 实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,
几何平均收益率的例子 例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%,第2年的投资收益率则为-50%。 实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,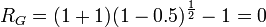 。这个计算结果符合实际情况,即两年来平均收益率为零。 相关条目 平均收益率算术平均收益率时间加权收益率实际收益率期望收益率
。这个计算结果符合实际情况,即两年来平均收益率为零。 相关条目 平均收益率算术平均收益率时间加权收益率实际收益率期望收益率
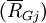 为:
为: 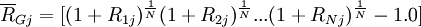 如果每个观察值的可能性不同,Pij是第i个收益率的概率,那么几何平均收益率为:
如果每个观察值的可能性不同,Pij是第i个收益率的概率,那么几何平均收益率为: 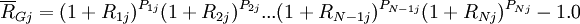 用符号
用符号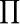 表示乘积,上式可写为:
表示乘积,上式可写为: 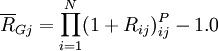 几何平均收益率的例子 例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%,第2年的投资收益率则为-50%。 实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,
几何平均收益率的例子 例如,某种股票的市场价格在第1年年初时为100元,到了年底股票价格上涨至200元,但时隔1年,在第2年年末它又跌回到了100元。假定这期间公司没有派发过股息,这样,第1年的投资收益率为100%,第2年的投资收益率则为-50%。 实际上,投资者尽管进行了两年的股票投资,但他的实际财富情况并未发生任何变化,其净收益为零。采用几何平均收益率来计算,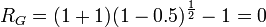 。这个计算结果符合实际情况,即两年来平均收益率为零。 相关条目 平均收益率算术平均收益率时间加权收益率实际收益率期望收益率
。这个计算结果符合实际情况,即两年来平均收益率为零。 相关条目 平均收益率算术平均收益率时间加权收益率实际收益率期望收益率
本文采摘于网络,不代表本站立场,转载联系作者并注明出处
